Close

A note on cookies

We use cookies to improve your experience of our website. If you want to find out more see our Privacy Policy

Menu

SIG Numerical Optimisation with Fluids

Events menu
Home / Events / Adjoint Methods / 

An introduction to gradient-based optimisation, adjoint methods and Automatic Differentiation

Summer School, Cambridge, 8-10 August 2018

blah
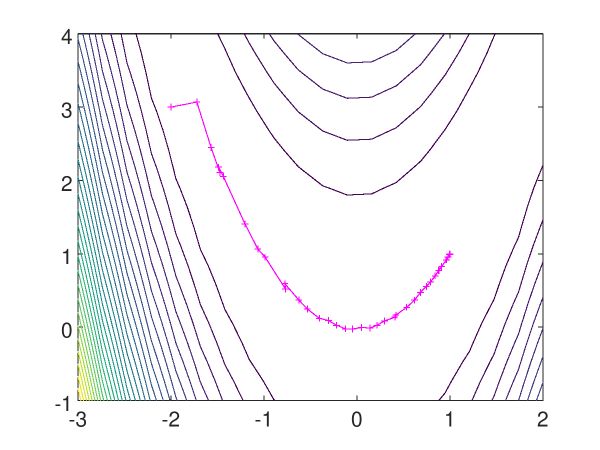
Minimising Rosenbrock's function with a Quasi-Newton method

Gradient-based optimisation methods are accepted as the most efficient optimisation algorithms for systems with large numbers of design or control variables. In particular, the adjoint-approach has become the most interesting approach in numerical optimisation using Computational Fluid Dynamics (CFD) and other computationally expensive systems governed by partial differential equations (PDEs) due to their low computational cost: a single adjoint solve allows to compute the gradient vector of a scalar objective function with respect to an arbitrarily large number of design or control variables.

This course will introduce

  • the important concepts of gradient-based optimisation,
  • the adjoint method
  • and how to use Automatic Differentiation to compute the required gradients.

Venue, Cost, Registration

The Summer School will be held at the Engineering Department of Cambridge University:

James Dyson Building Meeting Room, Engineering Department, Trumpington Street, Cambridge, CB2 1PZ.

The Summer School is free to attend. Attendees are expected to organise their own accommodation, lunches and coffee breaks will be provided.

To register, please follow this link.

Presenter

The Summer School will be taught by Dr. Jens-Dominik Müller, Queen Mary University of London

Training Code

Attendees are expected to bring their own laptop. The following software need to be installed: Octave, Fortran compiler.

Schedule

Topics will cover (program subject to change):

Wednesday 8 Aug

11:00-13:00 1: Overview and monovariate algorithms

  • Overview: what is it, what can it do, what are the benefits, where are the difficulties Examples. Stochastic vs. gradient based optimisation. Advantages of gradient-based optimisation in CFD, issues with industrial application. Lecture notes.

  • Monovariate gradient-based algorithms: secant method, Newton’s method. Lecture notes.

13:00-14:00 Sandwich lunch, provided

14:00-15:00 1.1: Practical on mono-variate algorithms

Octave practical on minimisation of mono-variate functions. Tutorial examples.

15:00-15:30 Coffee break

15:30-16:30 2: Multi-variate algorithms and safeguarding

  • Extension of basic methods to multivariate algorithms: Steepest Descent, Newton’s method. Lecture notes.

  • Safeguarding with line-searches and trust regions.

  • Congjugate Gradient, Quasi-Newton, SQP.

16:30-17:00 2.1: Practical on multi-variate algorithms

Octave practical on minimisation of multi-variate functions. Tutorial example.

Thursday, 9 August

09:00-11:00 3: Numerical Optimisation: constraints

11:00-11:30 Coffee break

11:30-12:00 3.1: Practical on algorithms for constrained optimisation

Octave practical on minimisation of constrained functions using penalty and barrier methods.

12:00-13:00 5: Algorithmic Differentiation and AD Tools

  • Algorithmic Differentiation, forward mode. Lecture notes.

  • Exercise: forward-mode differentiation

  • AD: reverse mode

  • Exercise: reverse-mode differentiation

  • Automatic differentiation with AD tools

13:00-14:00 Sandwich lunch, provided

14:00-15:00 5.1: Practical with AD Tools

Source-transformation using Tapenade’s online interface. Sample files.

15:00-15:30 Coffee break

15:30-17:00 4: Introduction to adjoint methods

  • Discrete vs continuous adjoints, gradient computation. Lecture notes.

  • Physical meaning of adjoint fields

  • Examples of sensitivity fields

  • Adjoint of the convection-diffusion equation

Friday 10 Aug

9:00-10:30 6: Adjoint CFD codes

  • Overview of application of AD to CFD codes,

  • Overview of major open-source CFD adjoint codes

11:00-11:30 Coffee break

11:30-13:00 6.1: Practical on adjoint optimisation

Fortran practical on minimisation of pde-constrained minimisation in forward and reverse mode. Exercises.

13:00-14:00 Sandwich lunch, provided

14:00-15:30 7: Parametrisation for shape optimisation

  • Overview of methods: lattice based, free-form deformation, radial-basis function. Lecture notes.

  • Node-based parametrisations, regularisation, preconditioning.

  • CAD-based parametrisations

^ Back to Top